어떤 규칙에 따라 실을 감아서 별 모양을 만든다거나 톱니바퀴를 따라 돌리면서 대칭적인 곡선을 그리는 디자인에서 최대공약수와 최소공배수의 원리를 찾아볼 수 있다.
1. 별 그림 속의 최대공약수
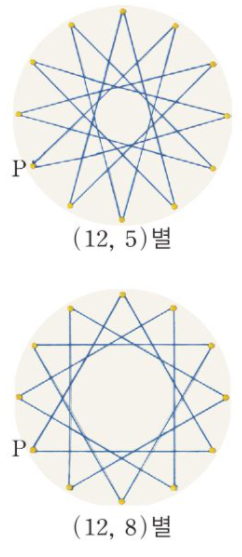
그림의 원 위에 일정한 간격으로 12개의 점을 찍고 한 점 P에서 시작하여 시곗바늘이 도는 방향으로 5번째에 있는 점을 차례대로 계속 선분으로 연결하여 만든 별 모양의 도형이다. 이 별 그림을 (12, 5)별과 같이 나타내기로 한다.
이 별 그림은 두 점을 연결한 선분이 계속 이어지면서 출발점으로 되돌아오게 되는데, 12와 5가 서로소이기 때문이다.
한편, (12, 8) 별을 그리면 오른쪽 그림과 같은데, 이 경우에는 분리된 4개의 정삼각형을 그리게 된다. 그 이유는 한 점에서 시곗바늘이 도는 방향으로 8번째 점을 연결하는 것은 반대 방향으로 4번째 점을 연결하는 것과 같으므로 세 번 만에 출발점으로 되돌아오기 때문이다.
이 별 그림에서 만들어지는 4개의 정삼각형에서 4는 12와 8의 최대공약수임을 알 수 있다.
2. 회전그래프 속의 최소공배수

그림은 톱니의 수가 각각 72와 39인 톱니바퀴 2개로 이루어진 회전그래프이다. 작은 톱니바퀴를 돌리면 펜의 위치에 따라 여러 가지 곡선이 그려지는데, 작은 톱니바퀴가 24바퀴 회전하면 처음 위치로 되돌아오게 된다.
작은 톱니바퀴의 톱니 수 39와 회전수 24를 곱하면 936인데, 이것은 톱니의 수 72와 39의 최소공배수이다.
(출처: Albert, B. B. JR., L. Ted, N., [Mathematics for Elementary Teachers])
출처
수학1 15개정 중등 교과서, 미래엔
'이런저런 이야기 > 수학' 카테고리의 다른 글
| 지식 곡선: 로지스틱(logistic) 곡선 (0) | 2021.09.16 |
|---|---|
| 망각 곡선 (0) | 2021.09.12 |
| 에라토스테네스의 체 (0) | 2021.09.05 |
| 하노이의 탑 (Tower of Hanoi) (0) | 2021.02.21 |
| 곱셈과 나눗셈 기호의 유래 (0) | 2021.02.21 |